・・・こんばんわ〜・・・ぐぅ、、、って、もう朝ぁ〜?
んじゃ、オッハ〜〜。。。ねむくてねむくて、死にそうだぉ〜。
前回の回帰分析で、経験値の予測をやったでしょ。
あれを見て、「そっかぁー、三日で3000ポイント突破かー」って思ってホントにやってみたんだけど。。。
ぜんっっっっっぜん、足りないっ!
半分の1500ポイントでストップしちゃったの。
かっ、勘違いしないでよね、これは科学的な検証なんだからっ。
べっ、別にゲームを始めたら、おもしろくって、はまって、止められなくなっちゃって、
学校行くのもお仕事も忘れて3日も徹夜しちゃったんじゃないんだからねっ!
くくぅー、、、そーだよねー・・・
もし、未来がぜーんぶ直線上にのっかってたら、予言なんてメチャかんたんだよね〜。
ってなことで、今日のテーマは「直線だけじゃない、いろんなパターンの回帰分析!」
ぐぅ、、、。
指数関数ねずみ算 対数関数人の慣れ 変化は微分で記述する
直線たったの1次式 変化するのは2次3次
次数どんどん上げてけば 精度どんどん上がってく 万能なのは多項式
必殺テイラー展開で どんなカーブも描けちゃう
判断ものさしAIC モデルは意味とデータから
まずは屈辱の経験値データ・・・やっぱ見る?
見せなきゃだめなんだよね、これは科学なんだから。。。(グッスン)
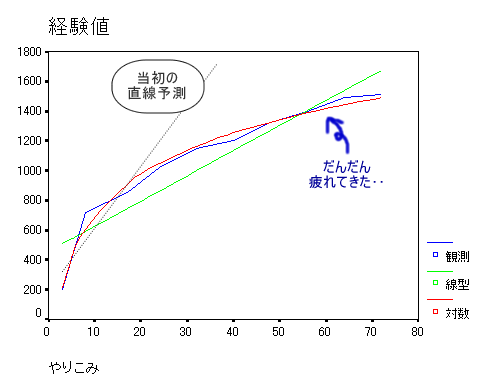
そのうちだんだんハイになってきて、頭がポワ〜ンってなっちゃったんだよね。
それが2日目にはモヤモヤ〜って感じになって、ほとんど進まなくなっちゃったの。
直線回帰予測では「時間をかけるほど -> 経験値が上がる」って単純に思ってたんだけど、
実際には「後に行くほど、経験値は上がりにくくなる」ってことだったんだね。
それじゃあ、この「後に行くほど上がりにくい」って関係を、数学では何と言うでしょう?
えーっと、比例の反対だから、反比例、かな?
おしい、ちょっと違うんだ。
反比例っていうのは「後に行くほど、減ってゆく」ことでしょ。
経験値がどんどん減っていったら、悲しいよね・・・
そうじゃなくって、経験値は「後に行くほど、増え方が、減ってゆく」の。
反比例して減ってゆくものを、積み重ねるってこと。
反比例っていうのを式にすると、
えー、わかんなーい、、、って、こんなのその場で考えたってわかんないよ、ふつー。公式覚えてるかどうかだけ。
なので3日後の経験値は、直線じゃなくて、対数で予想した方がよかったんだ。
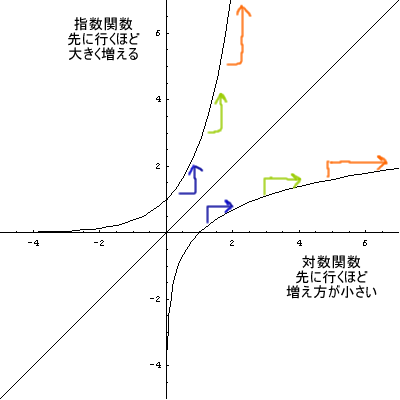
「対数」って、あまり普段使わないし、イメージ湧かないよね。
学校では、たぶん「指数の逆」だって教わるんだけど・・・
x = log[a] y と書いて、これを対数と定義する。
ミクのイメージだと、対数っていうのは「後に行くほど、増え方が減ってゆく」関係のこと。
ほら、映画やゲームがヒットすると、続編で2とか3とか、出てくるでしょ。
でも2のインパクトって、たいてい初代より小さいよね。
で、3のインパクトは、2より小さい。
それが4とか5とかになると、もうアンタしつこく何やってんの?って感じ。
でもこれって、制作スタッフが手抜いてるんじゃなくって、
2で1と同じことやってるだけだと、1より評価が下がっちゃうんだ。
1と同じ評価になるためには、1の何倍も良くないといけないの。
ってな感じで、リメイクを重ねるにつれて、インパクトがどんどん小さくなってゆくっていうのが対数のイメージ。
その対数が、学校で教わるように「指数の逆」になっていることの方が、むしろ不思議。
それには秘密があるんだ。
指数って何だろう。
簡単に言えば「ねずみ算」のこと。
親ねずみが10匹の子供を産んで、次の月に10匹の子供が10匹ずつ子供を産んで、
その次の月に全部の子供がまた10匹ずつ子供を産んで・・・
ってな具合に、子供の数がどんどん増えてゆくのが指数関数。
ねずみは、1、10、100、1000、10000 ・・・って1桁ずつ増えてゆくんだ。※
月の数を x、ねずみの数を y にして式を書くと、
次の世代が、今いるねずみの数だけ増えるんだから、
指数っていうのは、
増え方が、そのときの数(y)に比例して増える関係 のこと。
そうすると、対数との関係が見えてくるんじゃない?
対数っていうのは
増え方が、そのときの数(x)に反比例して増える関係 のこと。
ほら、なんか逆っぽいでしょ。
dy/dx = a y -- 増え方が、そのときの数に比例して増える関係
それは
y = C a ^ x -- 指数関数
だったときです。
対数:
dx/dy = (1/a) x -- 上の指数の式の x と y を逆にしてみました
dy/dx = a / x -- 増え方が、そのときの数に反比例して増える関係
それは
y = a ln | x | + C -- 対数関数
だったときです。
(C は不定な定数、とりあえずなんでもいい数ってことだよ)
記号で書くと dy/dx 。
増え方がわかっているとき、全体の関係がどうなるかっていうのは、積分するとわかるの。
こういうのを「微分方程式」って言うんだ。
でもって、指数・対数の考え方が、微分方程式の基礎中の基礎になってるんだね。
|
さて、ここまでで未来予測のパターンは3つ出てきたよ。
直線、指数、対数。
これで終わりなの?
そんなことないよね。
未来の変化パターンは無限にあるんだから、どんなにたくさん数式を作ってもカンペキにはならないの。
だったら、未来予測なんて無駄じゃない?
そうかなー。
たとえば12色しかない色鉛筆だって、無限の色の風景を描くことができるじゃない。
同じように、いくつかの知ってるパターンを組み合わせれば、それなりに未来予測できるんじゃないかな。
それじゃあ回帰分析の色鉛筆は、いったい何色あるんだろう。
もちろんたくさん知ってるほど、たくさんの色が使えるんだけど、最低限はずせないのは「2次式」かな。
放り投げたボールは「放物線」を描いて飛んでゆくでしょ。
あの放物線は、数式で言えば2次式。
重力みたいに一定の力で引っぱっているときは、グラフは放物線のようなカーブになるんだ。
なぜ「2次」っていうんだろう?
それは、物体の位置=0次、物体の速度=1次、物体の加速度=2次になっているから。
一定の力で引っぱってるってことは、加速度が一定、だから2次式。
2次があるってことは、その上に3次だってあるんだ。
もし重力が一定じゃなくて、下に行くほど強くなってゆくみたいに変化していたら、
放り投げたボールは三次式になって飛んでゆくはず。
そのときは、加速度の変化、だから「加加速度」ってことになるかな。
その上は、加加加速度=4次、加加加加速度=5次、加加加加加速度=6次、加加加加加加・・・いててっ、舌かんじゃった。
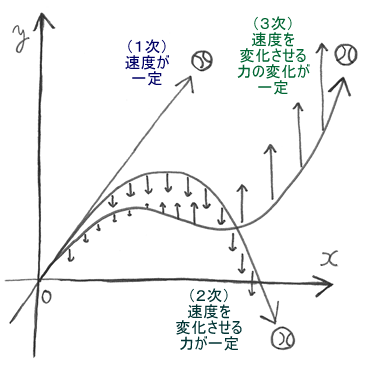
いま、加速って言ったけど、実際のN次式には加速だけじゃなくて減速もありなの。
式の上では、+プラスが加速になって、−マイナスが減速になるんだ。
例えば
最初は +5 で前進しているけど、-3 の力でだんだんブレーキがかかってきて、
そのうちストップして、今度は反対方向に動き出すの。
つまりこれは、ボールを上向きに放り投げたときの運動だね。
これのどこが必殺技なのか?
いま、2つの数字の加減速でもって、行って帰ってくるカーブが描けたよね。
この調子で、加減速をうまーく調整すれば、どんな形のカーブだって描けちゃうの!
まず速度を決めて、(1次)
カーブさせたかったら加減速を調整して、(2次)
ちょっと加速し過ぎたかな、と思ったら「加加速度」=加速度の変化を調整して、(3次)
それで減速し過ぎちゃったかな、と思ったら、今度は「加加加速度」=加速度の変化の変化を調整して・・・(4次)
これをどこまでも続ければ、最終的にはどんなカーブだってN次式に収まっちゃうんだ。※
どんな形のカーブも無限次の式で表せる、これがN次式の必殺技。
名付けて「テイラー展開っ!」( ← 必殺技っぽく、気合いと共に叫ぼう!)
例えば5次式のカーブが描きたかったら、とにかく
あとは、a〜f の6つのパラメータを決めれば予測が完成ってこと。
こういうやり方を、まとめて「多項式回帰」って呼んでるよ。
|
必殺、テイラー展開っ!
でもって、多項式っていうのは次数を大きくすれば、いくらでも精度が上がってゆくの。
2つの点があったら、両方を通る直線(=1次式の線)は1本だけ引けるよね。
同じように、3つの点を通る2次曲線は一本だけ引けます。
4つの点を通る3次曲線は一本だけ引けます。
5つの点を通る4次曲線は一本だけ引けます。
・・・
この調子で、もし1000個の点があったら、それをピッタリ結ぶ999次曲線が計算できちゃうの。
でも、それって意味あるのかな?
999次曲線って、1000個のパラメータがあるんだよ。
そんなの1000個のデータをそのまま並べたのと、変わらないじゃない。
999次曲線カンペキです、誤差が全然ありません!
・・・っていわれても、それで1001個目の点がピッタリ予測できるかっていうと、そんなことないよね。
1000個のデータの中には、本当に意味のある傾向と、今回たまたまそうなっただけの偶然が混じっているでしょ。
予測っていうのは、データの中から偶然を切り捨てて、意味のある傾向だけを取り出す作業。
じゃあ、どこに意味があって、どこが偶然なのか?
残念ながら、それは公式やコンピューターなんかじゃ見分けがつきません。
「この流れには、こんな力が働いてるんじゃないかな」って、元のデータの意味を考えるしか無いの。
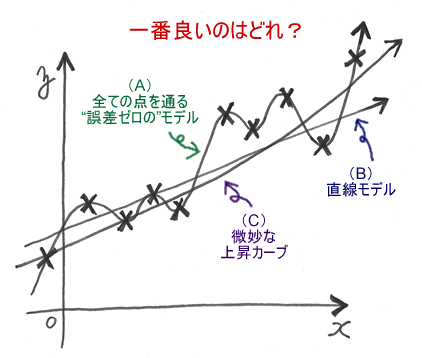
・モデル2: 長時間プレイすると疲れてくるから、後の方ほど経験値は上がりにくい。
・モデル3: もっとたくさんゲームをプレイすると、コツを掴んできて、経験値の上がりが早くなる。
・モデル4: 大人になったら、だんだんゲームってものに飽きてくるのかな?
モデル選びは試行錯誤。
データと意味との二人三脚で、いちばんピッタリするモデルを地道に探し出すの。
わけもわからず999次曲線とか作っても、なーんの役にも立たないぞ。
そうは言っても、どんな力が働いているのか、最初から分かっていれば何の苦労もないよね。
まだよく分かんないデータの中から、意味のある傾向を見つけ出すっていうのが、本当にやりたいことなんじゃないかな。
意味を見つけ出すのはコンピューターに100%お任せってわけにはいかないけど、
だいたいこの辺まで意味があるんじゃないかなっていう、モノサシみたいな公式ならあるんだ。
中でも一番有名なのが、赤池の情報量規準(Akaike's Information Criterion)、略してAIC。
なんかスパイみたいで、ちょっとカッコイイよね(そりゃCIA!)。
ずばり答を出しますよーってものじゃなくて、モノサシだから規準なの。
AICの考え方は、こんなの。
・できるだけ少ないパラメーターで、そこそこ正確な、ちょうどいい具合のところを見つけ出したい。
・そのために、精度とパラメーター数の両方を合わせたポイントを付けて、
ポイントが一番小さくなったときがベストってことにしよう。
n はデータの数、
ちょっと気になる 2π って数は、正規分布から出てくるの。
※ この計算には、誤差が正規分布だっていう前提が入ってます。
σ^2 はデータとモデルのずれを二乗して足したもの、
σ^2 = (1/n) Σ {(データの値) - (モデルから計算で出した値)} ^ 2
= (1/n) Σ {yi - (a x^m + b x^(m-1) + c x^(m-2) + ・・・)} ^ 2
とりあえず、良いモデルを探すためのモノサシがありますよー、ってことでいいと思うんだ。
|
そもそもモデルっていったい何だろう?
ぶっちゃけいうと、「数式で書けるものがモデル」なんです。※
・次に実際のデータにあてはまるようにパラメータを調整しましょう、
とにかく数式で書けさえすれば、あとは最小二乗法でパラメータを決めるだけ。
最小二乗法っていうのは、こんな方法でした。
・足し合わせた合計が一番小さくなるように、パラメータを調整する。
・具体的には、2乗して足し合わせた式を、それぞれのパラメータで微分する。
・パラメータの数だけ出てきた式を、連立方程式として解く。
たとえば指数モデルっていうのは、式に書くと
そのテクニックは、両辺の対数をとること。
= ln(a) + b x
ln(a) = A
こんな感じに、うまく直線と同じ形に持ち込めればラッキー。
それがダメでも、直線と同じ手順で地道に計算すれば、たいていの数式で予測パラメータが調整できちゃうんです。
|
未来は直線だけじゃない、いろんなモデルがあるってこと。
なんとなーくわかってくれたかな?
未来予測に大切なのは、なんといってもモデル選び。
基になるモデルが違っていたら、その先の結果も別物になっちゃうんです。
でも、モデルを自動的に選んでくれるような万能公式はありません。
データの意味を考えて、試行錯誤するしかないの。
で、そのときになって、この数式にはこんな意味があるんだなーっていうイメージが無いと、こまっちゃう。
イメージには正解が無いし、教科書にも書けません。
アタリマエの人にとってはアタリマエで、知らない人にとってはぜんぜんわからない。
なので、アタリマエの人がやってるのを見て、そんなものかなーって感じ取るのが一番だと思うの。
さて、今回はいろいろ盛りだくさんだったね。
頭にぎゅう〜っと詰め込んだら、なんだか眠くなってきちゃった・・・(徹夜3日目)
それじゃ、おやすみ〜、、、ぐぅ。