Здравствуйте!（ズドゥラーストヴィチェ）、ミクより愛をこめて。

毎日とっても充実してるかな？
どんなにステキなところでも、毎日毎日、いっつもおんなじだったら、飽きちゃうこともあるよね。
そんなときには、たまには「常識を破っちゃえ」って気分になっちゃうんだ。
ところが、おなじことくりかえしたらつまんなーい、っていうこの常識が、なんと破れちゃうことがあるんだよ。
今日お送りするのは、そんなプチ常識破りなの。
レッツ・シング・ア・ソング！

「大数の法則」って、聞いた事あるかな？
何回も何回も、たくさんくり返すと、だんだん平均に近づいてくるって法則。
ふーん、ミクが最初に聞いた時は、そんなのあったりまえじゃない、って思ったよ。
なんか、いちいち法則って呼ぶのが、ちょっと恥ずかしいかんじー。

でも、その後ずっとしてから、ミクは不思議な分布に出会ったの。
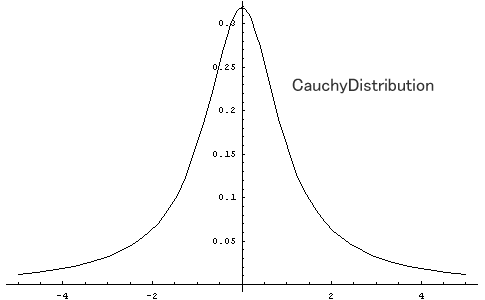
自由度が１のt分布、またの名前を「コーシー分布」。
グラフに書くと、左右が同じ形の、てれーんっとした丘って感じ。
あんまり特別には見えないの。

で、解説を見ると「コーシー分布には、中央値はあるけれど、平均値はありません。」って書いてあったんだよね。
ばっかじゃないの！
誰がどう見たって、まん中が平均に決まってんじゃん。
だって、右と左がまったく同じなんだよ。

でも、いちおー試してみるかなって思って、パソコンで調べてみたんだよね。
パ、パソコンが友達なんじゃないんだからねっ！
べつにあなたに友達になってもらわなくても、ミクにはたくさんお友達がいるんだからっ。
でも、どーしてもっていうんならー、お話してあげてもいいよ、特別にねっ。
で、コーシー分布の平均値っていうのを調べてみたら・・・
あれ、あれれ、毎回平均が違ってきちゃうぞ。
プログラムを実行するたびに、おっきくなったり、小さくなったり、
何度繰り替えしてもまん中のゼロに近付かないんだよね、これが。
プログラムの間違いかなって、何度も何度も見直したけど、そうじゃなくってやっぱり「平均値が無い」の。
ちょっとびっくり。
ってことは、世の中にはたくさん集めても平均に近付かない、常識破りの分布があったんだ。
大数の法則破れたりっ！
逆に言えば、「大数の法則」は常識でも当たり前でもない、特別なことだったんだね。
昨日出てきた「中心極限定理」も、やっぱりコーシー分布だと上手くいかないの。
常識破りのすごいやつだね。

じゃあ、なんでこのコーシー分布が特別なんだろう。
その秘密を探っちゃえ！
コーシー分布の式って、こんな風になってるの。

πってとこが気になっちゃうけど、これは決まりきった定数なんだから、この際無視しちゃってね。
確率分布の大事なところは、裾野がだんだん小さくなってゆく、その広がり具合。
ぜんぶ合わせると100%になってるはずだから、裾野がどんどん小さくなってかないといけないの。
コーシー分布は、積分すると 1/π[tan^-1(x)] ってなるから、たしかに無限におっきくはならないね。
なにこれ、ぜんっぜんわかんない？
きっときみは高校生のときにサボってたでしょ。
そんなはずはないんだけどなー・・・って、こんなの大人になって覚えてる人、どれだけいるのかな。
高校生って、大人が思ってるよりずーっと難しいことやってるんだゾ！
高校生までパーフェクトだったら、はっきりいって、いまミクの話なんて聞いてないはずだよね〜（ずがびーん！）
あっ、今高校生以下の人は、ぜんぜんＯＫだよ。
あと、今でも「気分は高校生」の人も、ぜんぜんおっけー！

さて、お次にコーシー分布の平均値を計算したら、どうなるかな。
確率分布の平均値っていうのは、くじが平均してどれだけ当るかなってこと、つまり期待値と同じだね。
たとえば確率50%で１０点だったら、50%ｘ１０点で５点。
もとの f(x)に、もう１つxをかけ算すると点数が出てくるの。
だから、期待値の式はこんな風になっちゃいます。

これを足し合わせてくと∫x/(1+x^2)dx は 1/x っぽくなるから、
どこまでもおっきくなっていって、無限の彼方に飛んでっちゃうの。
無限の彼方にいっちゃってるってことは、データはどこまでも広く散らばってるってこと。
どこまでも、無限に広く散らばっているんだから、その中で平均はここですって、決められないんだ。
ほら、宇宙が無限に広かったら、ここがまんなかですよーってところが無いでしょ。
それと同じ。
えっ、おれ様が中心だって思ってた？
何いってんのよ！（どげしどげしっ！）
宇宙の中心は、あたしに決まってるじゃない！

さてと、コーシー分布の秘密がだんだんわかってきたよね。
全然わからないですって？
なーにいじけてんのよ、難しい計算のとこは、そんなもんかなーって感じでいいの。
大切なのは「データはどこまでも広く散らばってる」ってとこ。
分散が有限じゃないと、まんなかに集まってくるってこともないからね。
分散って、データがどれだけ散らばっているか、データが離れている「平均距離」のことだったよね。
これ、思ったより大事なものだったんだねー。
データは普通たくさんあるから、どれだけのデータが分散の中に入ってきてるかって目安が大切になってくるよね。
この目安を式にしたのが「チェビシェフの不等式」。

げげーっ、難しそーな式っ・・・
って、実はそれほどでもないの。
１つずつ意味を追ってみるね。
P は確率、Probability の P。
P() は、カッコの中になる確率は、って読むの。
μは平均、だから |x-μ| は、平均からデータまでの差ってこと。
もし平均がゼロだったら、|x| だけでいいよ。
σ は偏差、つまり √(分散)ってことだね。
この σ が、データが離れている平均距離。
a には好きな数を入れていいの。

実際にチェビシェフの不等式を使ってみるよ。
平均μはこのさいゼロってことにしちゃって、a に 2 って数を入れてみると、

これは「データが偏差の２倍より離れている確率は、1/4 以下です」って読むんだ。
a を 3 にしたら「データが偏差の３倍より離れている確率は、1/9 以下です」ってなるね。
なんでこうなるんだろうって悩んじゃうより、これってほとんど分散の意味なんだって考えた方が楽。

でもでも、なぜだろうって、どーしても気になっちゃう？
どーしてもっていうんならー、教科書丸写ししないこともないんだけどー、ほんとに見る？
じゃ、覚悟してね。
x が aσ より遠いところでは、言葉通りに x^2 >= (aσ)^2 になるでしょ。（２乗しただけだよ）
分散って、x^2 f(x) を足し合わせたもの、つまり積分だから、

両辺を (aσ)^2 で割って、
これがチェビシェフの不等式そのもの。
ううっ、式だらけ・・・聞かない方がよかったかなー。
でも１こ１こ見てくと、そんなに難しくないんだから、あせらないあせらない。

さて「チェビシェフの不等式」がわかったところで、
・・・わかんなくても、そんなものかなーって思ったところで、
あたりまえでない「大数の法則」の謎を解くよ。

大数の法則の本当の秘密は「データがたくさんあるほど、ばらつきが小さくなってくこと」にあるんだ。
つまり、分散はデータの数に反比例して小さくなってくってこと。

V^2 って書いたのは、よくわかんないんだけど、「データのばらつきの大元になる真の値」ってことにするね。
なにか元になるものがあって、そこからｎ個データをとってきたら、ばらつきは 1/n になりますよって意味。
（ここんとこ、詳しくは「第１０話　ちょっぴりちがうの標本は、不偏分散」にもう一度出てくるよ。
　今はよくわかんなくても、そんなものかなーっていうのでＯＫ。）

ここでもういちど、チェビシェフさんのご登場。

この中の σ を式の右側にもってきたいから、aσ ってところをまとめて ε って記号に書き直すね。
すると、
ってなるね。
これってただ記号を置き換えただけ。

次は、分散のところを「ばらつきが小さくなってく」って感じにしちゃうんだ。
先に出てきた「真の値」、V^2 の式をあてはめちゃうと、

さあ出てきたぞ、これが答の式なんだ。
えっ、どこどこって、よーくこの式を読んでみよーよ。
ヒントは、εを「ゆらぎ」と読む。
P が付いてる式の左側は、「確率が平均値よりもεだけ外れているのは」って読むの。
ほんのちょっとだけゆらいでる確率ってこと。
式の右側は、データのばらつきはｎをどんどん大きくすると、ゼロになっちゃいますってこと。
全部合わせて「データがたくさんあるほど、ゆらぎが小さくなる」って読めるんだ。
うぐぅ、、、式だらけで死んじゃいそう・・・
だいじょーぶ、この程度じゃ死なない、死なない。

大切なのは、大数の法則は「あったりまえの常識」じゃなくて、ちゃんと理由があったんだってこと。
あたりまえに見えることでも、深く深ぁーく理由を探ってみると、毎日がとっても新鮮だよっ！
がんばれ、気分は高校生！

そんじゃね、Пока.（パカー）。